CAGED Part 3: Intervals

by

<< Goto CAGED Part 1: The CAGED System
<< Goto CAGED Part 2: The Major Scale

Viewing the Positions in Terms of Intervals

Now that we are familiar with the 5 positions and the major scale in each position the next step is to start to view each position in terms of intervals.

At some stage I’ll devote a full section of the site to intervals but for our purposes here, lets take a bit of a simplified look at what intervals are.

An interval is essentially the distance between two notes. You can see this distance as the number of frets between two notes on the same string.

Looking at the major scale on a single string, we could number the notes of the scale as follows:

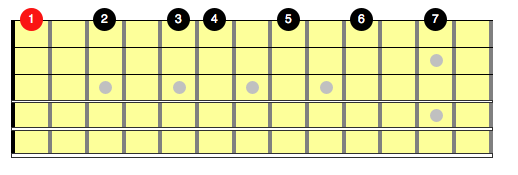
Each number here refers to an interval between the root note (the red dot) and the numbered note.

The names of these 7 intervals are as follows:

1: Unison
2: Major 2nd
3: Major 3rd
4: Perfect 4th
5: Perfect 5th
6: Major 6th
7: Major 7th

We can then number the notes not in the major scale by using the number of the major scale note that is 1 note up and putting a b (flat) in front of the number.

We then have:

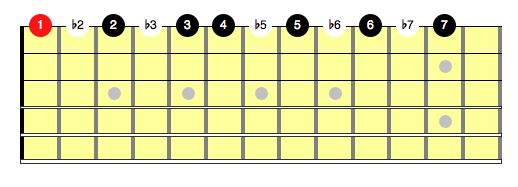
Each of these new flattened notes also forms an interval with the root of the scale. These intervals are called:

b2: minor 2nd
b3: minor 3rd
b5: diminished 5th
b6: minor 6th
b7: minor 7th

This same numbering scheme can be applied to the major scale in the CAGED system as well as the major scale on a single string. Looking at the major scale with the E shaped CAGED position we can number the notes as follows:

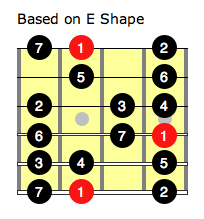
Note here that once we get to the 7th note, the next note is the root. We are only going to look at intervals in terms of their distance of a note to its next lowest root here so the numbering goes back to 1 and starts again for the next octave.

These numberings refer to the same intervals for the major scale on a single string but are simply placed across all strings in a position.

We can then go through this process and number the notes of the major scale relative to their root note for the other CAGED positions and we get:

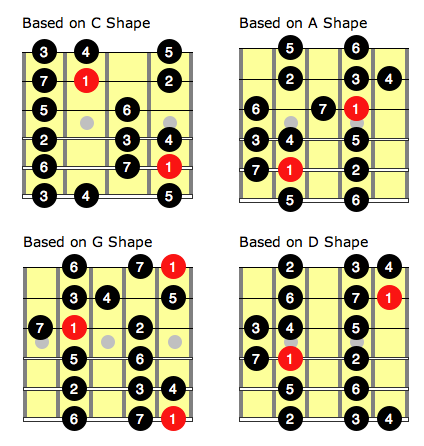
At this point you want to go back to the guitar and continue practicing your major scale in all 5 positions but you want to start to see each note you play in terms of the number here. You might want to play the scale slowly and think the number your playing to yourself as you play it, or even say it out loud. You could then practice this with the scale sequences and your own phrases based on the major scale.

This is best learned at the fretboard while playing the scale rather than trying to memorize it from the diagrams I’m showing. Use the diagrams to understand the concept and ingrain the numbers while playing the scale on the guitar.

Once you feel you have a good grasp of the number of each note, you need to recognise that the notes between the major scale notes are also our flattened notes. Similarly to when we formed these intervals on a single string, each number is the number of the major scale note that is a note up, but flattened.

In our CAGED positions, this then allows us to number all of the notes in all the positions as follows:

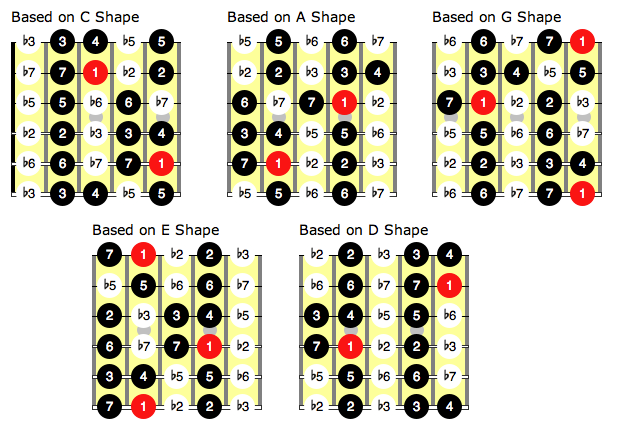
I’m providing these diagrams for you to understand the concept, but similarly to the major scale notes you want to start to recognise these flattened notes on the fretboard while playing rather than memorising the diagrams. Use what you’ve learned with the major scale as the basis and recognise the flattened intervals by the major scale note next to the interval.

We have now looked at each CAGED position in terms of the intervals that comprise each note in the position relative to the root note of the position. A proper treatment of intervals would be a bit different that what I’ve presented here, but I think this is the best introduction for the purpose of seeing these intervals in the CAGED position.

Viewing Scales and Arpeggios in Terms of their Intervals

Using these intervals, you should be able to see that the major scale is constructed using the intervals 1, 2, 3, 4, 5, 6 and 7. It is possible to define any scale or arpeggio in terms of which of these intervals comprise the scale.

Lets look at the old faithful Minor Pentatonic.

It is composed of the intervals: 1, b3, 4, 5, b7

Using this and our interval knowledge of the CAGED positions, we can then form the pattern for this scale in each position. Take the E shaped position which we have seen has the intervals:

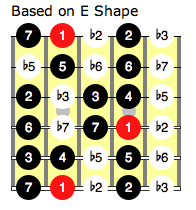
Now simply pick out the notes that are 1, b3, 4, 5, and b7 and we have our common minor pentatonic shape:

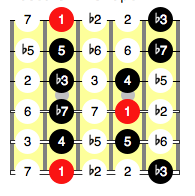
Remove the number from the chart and you have the familiar pattern:

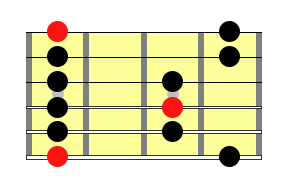
You can then apply this to all 5 positions to form the minor pentatonic shape in all CAGED positions all the way up the fretboard.

Lets take another example. Lets form the dorian in the C Shaped CAGED position.

The dorian is formed from the intervals: 1, 2, b3, 4, 5, 6, b7

The intervals of the C shaped CAGED position are:

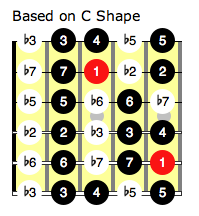
Filling in these dorian intervals here we have:

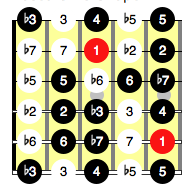
And if we remove the numbering from the chart we have a dorian scale as follows:

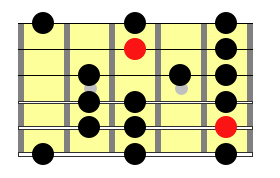
I hope this has illustrated how to form the pattern of any scale or arpeggio in any of the CAGED position by simply knowing the intervals that comprise the scale.

I would start to devote regular practice time to picking a different scale or arpeggio and figuring out the pattern for it in all 5 positions on the fretboard using your interval knowledge we ingrained with the major scale. This will not only allow you to form scale patterns yourself but also further ingrain your knowledge of the intervals in the CAGED positions while you do this.

You would then also treat the repetitive playing of the pattern to ingrain it as a different exercise but I see value to slowly constructing these patterns in its own right.

You should know the intervals that comprise any scale or arpeggio you learn as part of learning the scale and I’ll provide the interval formulas here of a number of scales and arpeggios so you can practice forming the patterns, then go on to practice the patterns if you want to also master the scale:

Major Scale: 1, 2, 3, 4, 5, 6, 7
Minor Pentatonic Scale: 1, b3, 4, 5, b7
Blues Scale: 1, b3, 4, b5, 5, b7
Natural Minor Scale: 1, 2, b3, 4, 5, b6, b7
Dorian Mode: 1, 2, b3, 4, 5, 6, b7
Mixolydian Mode: 1, 2, 3, 4, 5, 6, b7
Phrygian Mode: 1, b2, b3, 4, 5, b6, b7
Major Pentatonic Scale: 1, 2, 3, 5, 6
Harmonic Minor Scale: 1, 2, b3, 4, 5, b6, 7
Melodic Minor Scale (Jazz Form): 1, 2, b3, 4, 5, 6, 7
Phrygian Dominant Scale: 1, b2, 3, 4, 5, b6, b7

Major Arpeggio: 1, 3, 5
Minor Arpeggio: 1, b3, 5
Diminished Arpeggio, 1, b3, b5
Major 7th Arpeggio: 1, 3, 5, 7
Minor 7th Arpeggio: 1, b3, 5, b7
Dominant 7th Arpeggio: 1, 3, 5, b7

These formulas should provide ample material for you to practice forming the patterns in the CAGED positions from the formulas.

I hope this has been helpful!

<< Goto CAGED Part 1: The CAGED System
<< Goto CAGED Part 2: The Major Scale

by